Theoretical models

Of the four fundamental interactions, gravitation is dominant at cosmological length scales; that is, the other three forces are believed to play a negligible role in determining structures at the level of planets, stars, galaxies and larger-scale structures. Since all matter and energy gravitate, gravity's effects are cumulative; by contrast, the effects of positive and negative charges tend to cancel one another, making electromagnetism relatively insignificant on cosmological length scales. The remaining two interactions, the weak and strong nuclear forces, decline very rapidly with distance; their effects are confined mainly to sub-atomic length scales.

General theory of relativity

Main articles: Introduction to general relativity, General relativity, and Einstein's field equations

Given gravitation's predominance in shaping cosmological structures, accurate predictions of the universe's past and future require an accurate theory of gravitation. The best theory available is Albert Einstein's general theory of relativity, which has passed all experimental tests hitherto. However, since rigorous experiments have not been carried out on cosmological length scales, general relativity could conceivably be inaccurate. Nevertheless, its cosmological predictions appear to be consistent with observations, so there is no compelling reason to adopt another theory.

General relativity provides of a set of ten nonlinear partial differential equations for the spacetime metric (Einstein's field equations) that must be solved from the distribution of mass-energy and momentum throughout the universe. Since these are unknown in exact detail, cosmological models have been based on the cosmological principle, which states that the universe is homogeneous and isotropic. In effect, this principle asserts that the gravitational effects of the various galaxies making up the universe are equivalent to those of a fine dust distributed uniformly throughout the universe with the same average density. The assumption of a uniform dust makes it easy to solve Einstein's field equations and predict the past and future of the universe on cosmological time scales.

Einstein's field equations include a cosmological constant (Λ),^[53][54] that corresponds to an energy density of empty space.^[55] Depending on its sign, the cosmological constant can either slow (negative Λ) or accelerate (positive Λ) the expansion of the universe. Although many scientists, including Einstein, had speculated that Λ was zero,^[56] recent astronomical observations of type Ia supernovae have detected a large amount of "dark energy" that is accelerating the universe's expansion.^[57] Preliminary studies suggest that this dark energy corresponds to a positive Λ, although alternative theories cannot be ruled out as yet.^[58] Russian physicist Zel'dovich suggested that Λ is a measure of the zero-point energy associated with virtual particles of quantum field theory, a pervasive vacuum energy that exists everywhere, even in empty space.^[59] Evidence for such zero-point energy is observed in the Casimir effect.

Special relativity and space-time

Main articles: Introduction to special relativity and Special relativity

Only its length L is intrinsic to the rod (shown in black); coordinate differences between its endpoints (such as Δx, Δy or Δξ, Δη) depend on their frame of reference (depicted in blue and red, respectively).

The universe has at least three spatial and one temporal (time) dimension. It was long thought that the spatial and temporal dimensions were different in nature and independent of one another. However, according to the special theory of relativity, spatial and temporal separations are interconvertible (within limits) by changing one's motion.

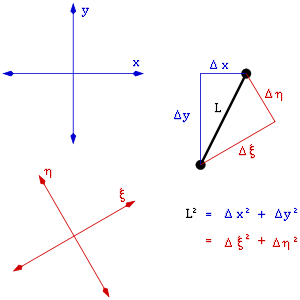
To understand this interconversion, it is helpful to consider the analogous interconversion of spatial separations along the three spatial dimensions. Consider the two endpoints of a rod of length L. The length can be determined from the differences in the three coordinates Δx, Δy and Δz of the two endpoints in a given reference frame

L² = Δx² + Δy² + Δz²

using the Pythagorean theorem. In a rotated reference frame, the coordinate differences differ, but they give the same length

L² = Δξ² + Δη² + Δζ².

Thus, the coordinates differences (Δx, Δy, Δz) and (Δξ, Δη, Δζ) are not intrinsic to the rod, but merely reflect the reference frame used to describe it; by contrast, the length L is an intrinsic property of the rod. The coordinate differences can be changed without affecting the rod, by rotating one's reference frame.

The analogy in spacetime is called the interval between two events; an event is defined as a point in spacetime, a specific position in space and a specific moment in time. The spacetime interval between two events is given by

where c is the speed of light. According to special relativity, one can change a spatial and time separation (L₁, Δt₁) into another (L₂, Δt₂) by changing one's reference frame, as long as the change maintains the spacetime interval s. Such a change in reference frame corresponds to changing one's motion; in a moving frame, lengths and times are different from their counterparts in a stationary reference frame. The precise manner in which the coordinate and time differences change with motion is described by the Lorentz transformation.